Understanding DeepONet: Learning Nonlinear Operators with Neural Networks
By Muyan Li, NEDMIL Research Group
Introduction
While reading the paper “Learning Nonlinear Operators via DeepONet Based on the Universal Approximation Theorem of Operators” (Lu et al., Nature Machine Intelligence, 2021), I gained a preliminary understanding of DeepONet. Below is a summary of my learning process and reflections.
What is DeepONet?
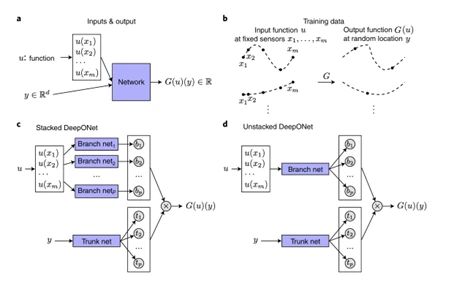
DeepONet (Deep Operator Network) is a neural network architecture based on the universal approximation theorem for operators. It is designed to learn nonlinear continuous operators, i.e. mappings from input functions to output functions. It consists of two subnetworks:
- Branch Network: processes the discrete values of the input function at fixed sensor locations.
- Trunk Network: processes the domain coordinates of the output function.
The outputs of these two networks are combined through an inner product to approximate the target operator.
Theoretical Basis of DeepONet
The theoretical foundation of DeepONet comes from the general approximation theorem for operators proposed in 1995. It states that a neural network with one hidden layer can approximate any nonlinear continuous operator (a continuous mapping from one function space to another) with arbitrary precision.
Mathematically, for any continuous nonlinear operator \( \mathcal{G} \) and any precision \( \varepsilon > 0 \), there exist positive integers \( p, m, n \) and real parameters such that for all input functions \( u \) and output coordinates \( y \),
\[ \mathcal{G}(u)(y) \approx \sum_{k=1}^{p} b_k(u)\,\tau_k(y) \]
where \( \mathcal{G}(u)(y) \) represents the output function at point \( y \), \( b_k(u) \) are coefficients dependent on the input function \( u \), and \( \tau_k(y) \) are basis functions associated with the output coordinates.
Key Components
The term \( \mathcal{G}(u)(y) \) denotes the target operator. For example, if \( \mathcal{G} \) is the solution operator of a differential equation, then \( \mathcal{G}(u) \) is the corresponding solution, and \( \mathcal{G}(u)(y) \) is the solution value at position \( y \).
The summation \( \sum_{k=1}^{p} \) represents a linear combination of \( p \) basis functions — similar to the number of neurons in a hidden layer. A larger \( p \) generally provides stronger approximation capacity.
The Branch Network: Processing the Input Function \( u \)
The branch network encodes the input function \( u \) into coefficients \( \{b_1, b_2, \dots, b_p\} \). The function \( u \) is sampled at \( m \) fixed sensor points \( \{x_1, x_2, \dots, x_m\} \), producing discrete input data.
Each coefficient \( b_k \) is computed using:
\[ b_k = \sum_{i=1}^{n} c_i^k \, \sigma\!\left( \sum_{j=1}^{m} \xi_{ij}^k u(x_j) + \theta_i^k \right) \]
where \( \sigma(\cdot) \) is a nonlinear activation (e.g., Tanh or Sigmoid), \( \xi_{ij}^k \) are weights, \( \theta_i^k \) are biases, and \( c_i^k \) are output layer weights. This architecture represents the “stacked” structure of the theoretical DeepONet.
The Trunk Network: Processing the Output Coordinates \( y \)
The trunk network provides the basis functions \( \tau_k(y) \) with respect to the output coordinates \( y \). For each basis function \( k \):
\[ \tau_k(y) = \sigma(w_k \cdot y + \zeta_k) \]
where \( w_k \) and \( \zeta_k \) are the weight vector and bias term, respectively. These outputs combine with the branch coefficients through an inner product to produce the final operator output.
Evolution of DeepONet: From Stacked to Non-Stacked
Stacked DeepONet
The original, or stacked, form of DeepONet directly follows the theorem: each coefficient \( b_k \) is computed by an independent branch sub-network. While mathematically sound, this structure is inefficient and parameter-heavy.
Non-Stacked DeepONet
To improve efficiency, researchers introduced the non-stacked DeepONet, which merges all branch sub-networks into a single, deeper network that outputs a vector \( [b_1, b_2, \dots, b_p]^{\top} \). This version enables parameter sharing, reduces redundancy, and improves generalization.
| Feature | Stacked DeepONet | Non-Stacked DeepONet |
|---|---|---|
| Number of branch networks | \( p \) | 1 |
| Branch output | Each net outputs one scalar \( b_k \) | Single net outputs vector \( [b_1,…,b_p] \) |
| Parameter sharing | None | Full |
| Parameter efficiency | Poor (linear growth with \( p \)) | High (shared weights) |
| Expressive power | Theoretical equivalence | Stronger in practice |
| Generalization | Risk of overfitting | Better due to regularization |
| Relation to theorem | Direct implementation | Efficient practical evolution |
From Theory to Practice
In theory, the stacked structure demonstrates that neural networks can approximate operators mathematically. The non-stacked version extends this concept through deeper architectures and shared parameters, transforming the branch network from a "committee" (independent voters) into a "brain" (collaborative learner).
Experiments show that non-stacked DeepONet achieves lower training error, better stability, and faster convergence while using fewer parameters. It has therefore become the de facto standard in research and applications.
Applications and Current Research
Most research has applied DeepONet to elliptic PDEs such as Poisson and Darcy flow equations. However, its application to parabolic PDEs (time-dependent systems) remains relatively under-explored.
Classical numerical methods — finite difference, finite element, and spectral methods — work well but face challenges for high-dimensional or parametric problems, complex geometries, and fast computations under varying conditions (the "curse of dimensionality").
DeepONet offers a new paradigm: it learns the entire solution operator across a family of equations, enabling rapid inference without re-solving each configuration.
At NEDMIL, my current work focuses on applying DeepONet to parabolic PDEs, assessing whether this framework can provide an efficient, generalizable solution for complex dynamic systems.
Summary
DeepONet is a neural network architecture designed to learn nonlinear continuous operators, bridging mathematical theory and deep learning. Its twin structure — the branch and trunk networks — makes it a powerful framework for learning mappings between functional spaces.
The transition from the theoretical stacked form to the efficient non-stacked architecture marks its evolution from mathematical proof to practical implementation. This efficiency has positioned DeepONet as a cornerstone of modern scientific machine learning.
Reference
Lu, L., Jin, P., Pang, G., Zhang, Z., & Karniadakis, G. E. (2021). Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nature Machine Intelligence, 3(3), 218–229. https://doi.org/10.1038/s42256-021-00302-5

